Skilled neural networks arrive at options that obtain superhuman efficiency on an growing variety of duties. It will be a minimum of attention-grabbing and possibly vital to know these options.
Attention-grabbing, within the spirit of curiosity and getting solutions to questions like, “Are there human-understandable algorithms that seize how object-detection nets work?”[a] This might add a brand new modality of use to our relationship with neural nets from simply querying for solutions (Oracle Fashions) or sending on duties (Agent Fashions) to buying an enriched understanding of our world by finding out the interpretable internals of those networks’ options (Microscope Fashions). [1]
And vital in its use within the pursuit of the sorts of requirements that we (ought to?) demand of more and more highly effective methods, equivalent to operational transparency, and ensures on behavioral bounds. A typical instance of an idealized functionality we might hope for is “lie detection” by monitoring the mannequin’s inner state. [2]
Mechanistic interpretability (mech interp) is a subfield of interpretability analysis that seeks a granular understanding of those networks.
One might describe two classes of mech interp inquiry:
- Illustration interpretability: Understanding what a mannequin sees and the way it does; i.e., what data have fashions discovered vital to search for of their inputs and the way is that this data represented internally?
- Algorithmic interpretability: Understanding how this data is used for computation throughout the mannequin to lead to some noticed end result
Determine 1: “A Acutely aware Blackbox,” the duvet graphic for James C. Scott’s Seeing Like a State (1998)
This submit is anxious with illustration interpretability. Structured as an exposition of neural community illustration analysis [b], it discusses varied qualities of mannequin representations which vary in epistemic confidence from the apparent to the speculative and the merely desired.
Notes:
- I’ll use “Fashions/Neural Nets” and “Mannequin Elements” interchangeably. A mannequin part might be considered a layer or another conceptually significant ensemble of layers in a community.
- Till correctly launched with a technical definition, I exploit expressions like “input-properties” and “input-qualities” instead of the extra colloquially used “function.”
Now, to some foundational hypotheses about neural community representations.
Decomposability
The representations of inputs to a mannequin are a composition of encodings of discrete data. That’s, when a mannequin appears to be like for various qualities in an enter, the illustration of the enter in some part of the mannequin might be described as a mixture of its representations of those qualities. This makes (de)composability a corollary of “encoding discrete data”- the mannequin’s capability to symbolize a set set of various qualities as seen in its inputs.
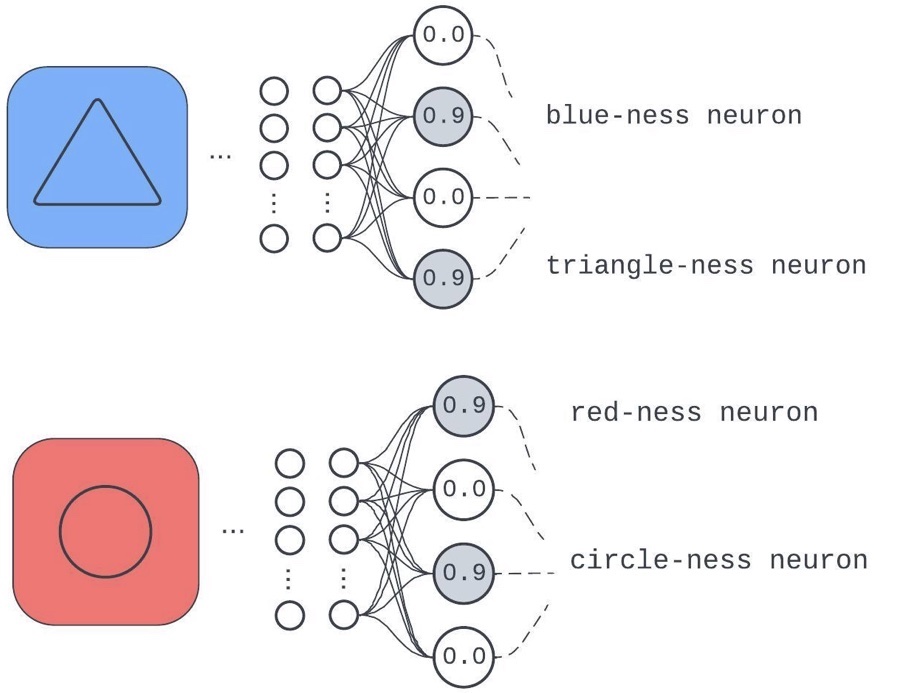
Determine 2: A mannequin layer educated on a job that wants it to care about background colours (educated on solely blue and crimson) and middle shapes (solely circles and triangles)
The part has devoted a special neuron to the enter qualities: “background shade consists of crimson,” “background shade consists of blue,” “middle object is a circle,” and “middle object is a triangle.”
Think about the choice: if a mannequin did not determine any predictive discrete qualities of inputs in the midst of coaching. To do nicely on a job, the community must work like a lookup desk with its keys because the naked enter pixels (since it may well’t glean any discrete properties extra attention-grabbing than “the ordered set of enter pixels”) pointing to distinctive identifiers. We have now a reputation for this in apply: memorizing. Subsequently, saying, “Mannequin elements study to determine helpful discrete qualities of inputs and compose them to get inner representations used for downstream computation,” isn’t far off from saying “Generally, neural nets don’t fully memorize.”
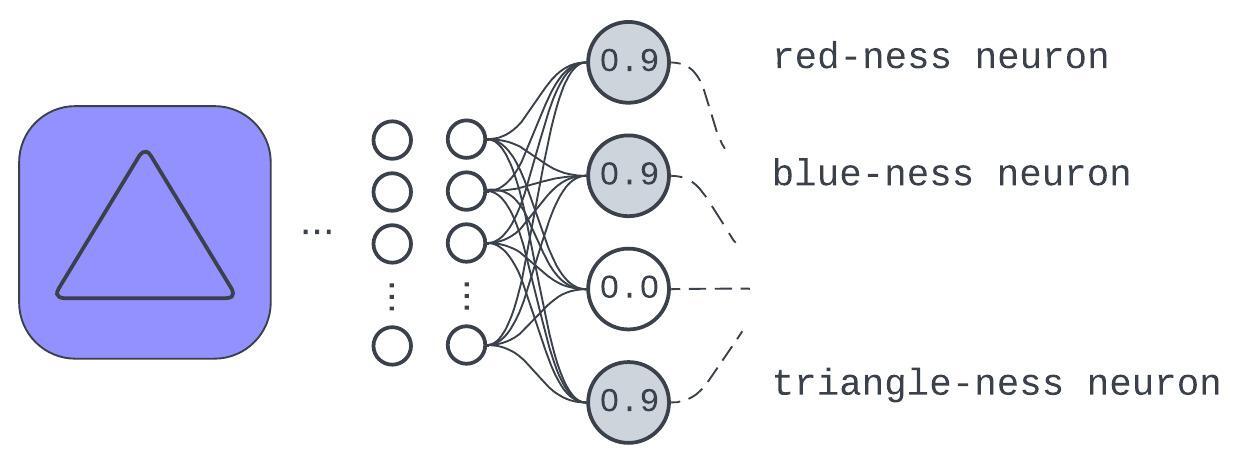
Determine 3: An instance of how studying discrete enter qualities affords generalization or robustness
This instance check enter, not seen in coaching, has a illustration expressed within the realized qualities. Whereas the mannequin won’t absolutely admire what “purple” is, it’ll be higher off than if it was simply making an attempt to do a desk lookup for enter pixels.
Revisiting the speculation:
“The representations of inputs to a mannequin are a composition of encodings of discrete data.”
Whereas, as we’ve seen, this verges on the apparent; it supplies a template for introducing stricter specs deserving of research.
The primary of those specification revisits appears to be like at “…are a composition of encodings…” What’s noticed, speculated, and hoped for in regards to the nature of those compositions of the encodings?
Linearity
To recap decomposition, we count on (non-memorizing) neural networks to determine and encode various data from enter qualities/properties. This means that any activation state is a composition of those encodings.
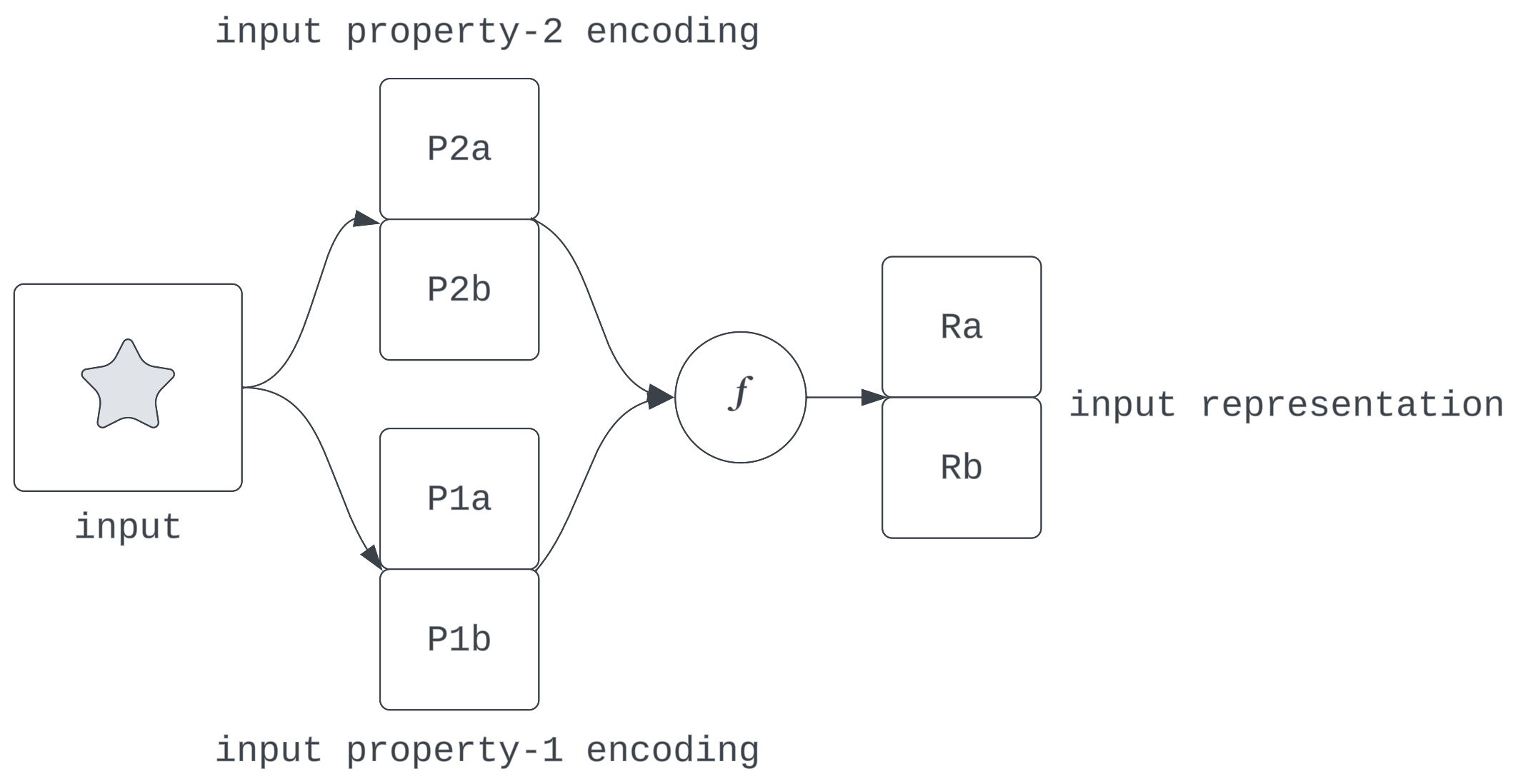
Determine 4: What the decomposability speculation suggests
What’s the nature of this composition? On this context, saying a illustration is linear suggests the knowledge of discrete enter qualities are encoded as instructions in activation house and they’re composed right into a illustration by a vector sum:
We’ll examine each claims.
Declare #1: Encoded Qualities Are Instructions in Activation Area
Composability already means that the illustration of enter in some mannequin elements (a vector in activation house) consists of discrete encodings of enter qualities (different vectors in activation house). The extra factor stated right here is that in a given input-quality encoding, we are able to consider there being some core essence of the standard which is the vector’s route. This makes any specific encoding vector only a scaled model of this route (unit vector.)
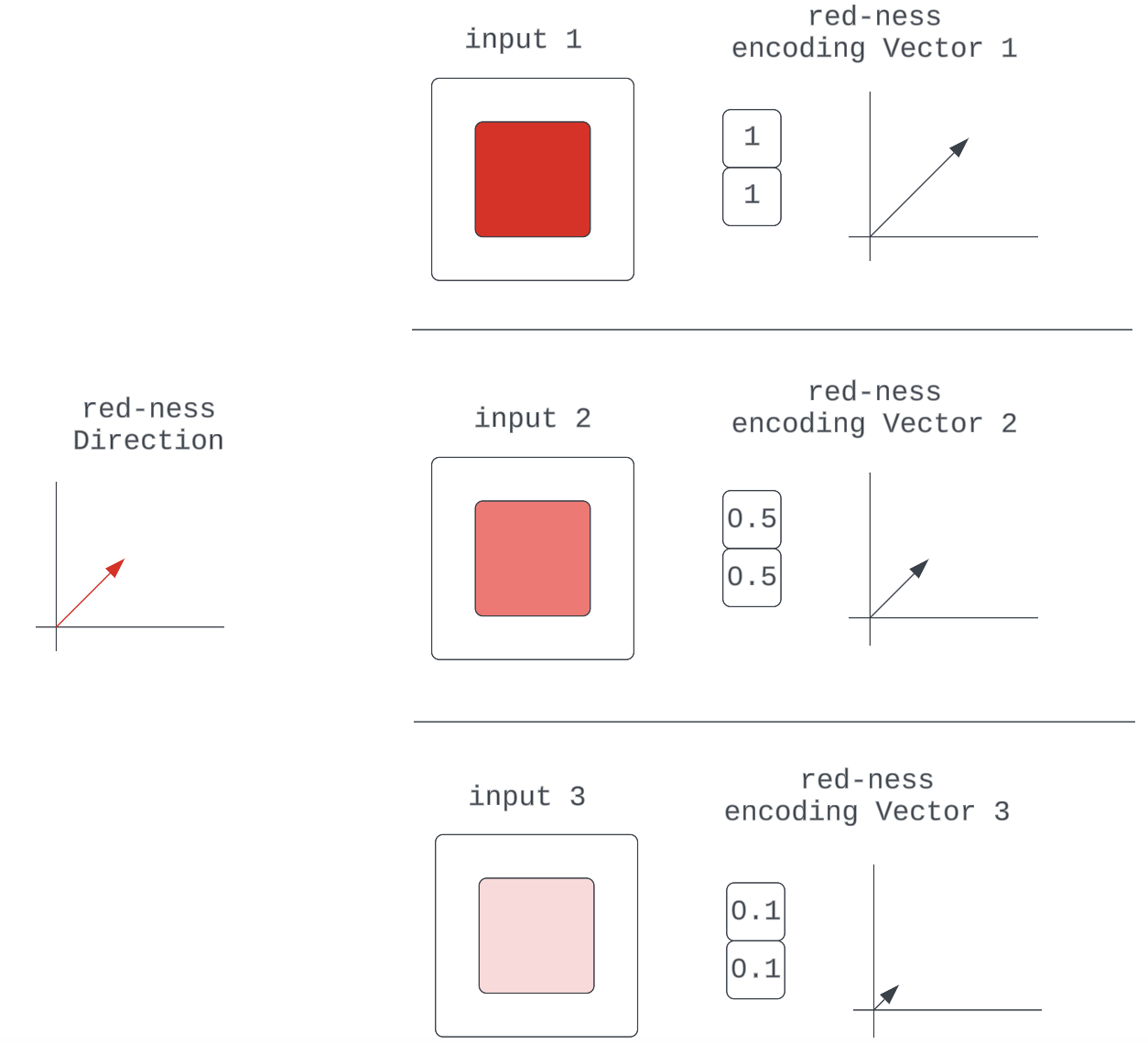
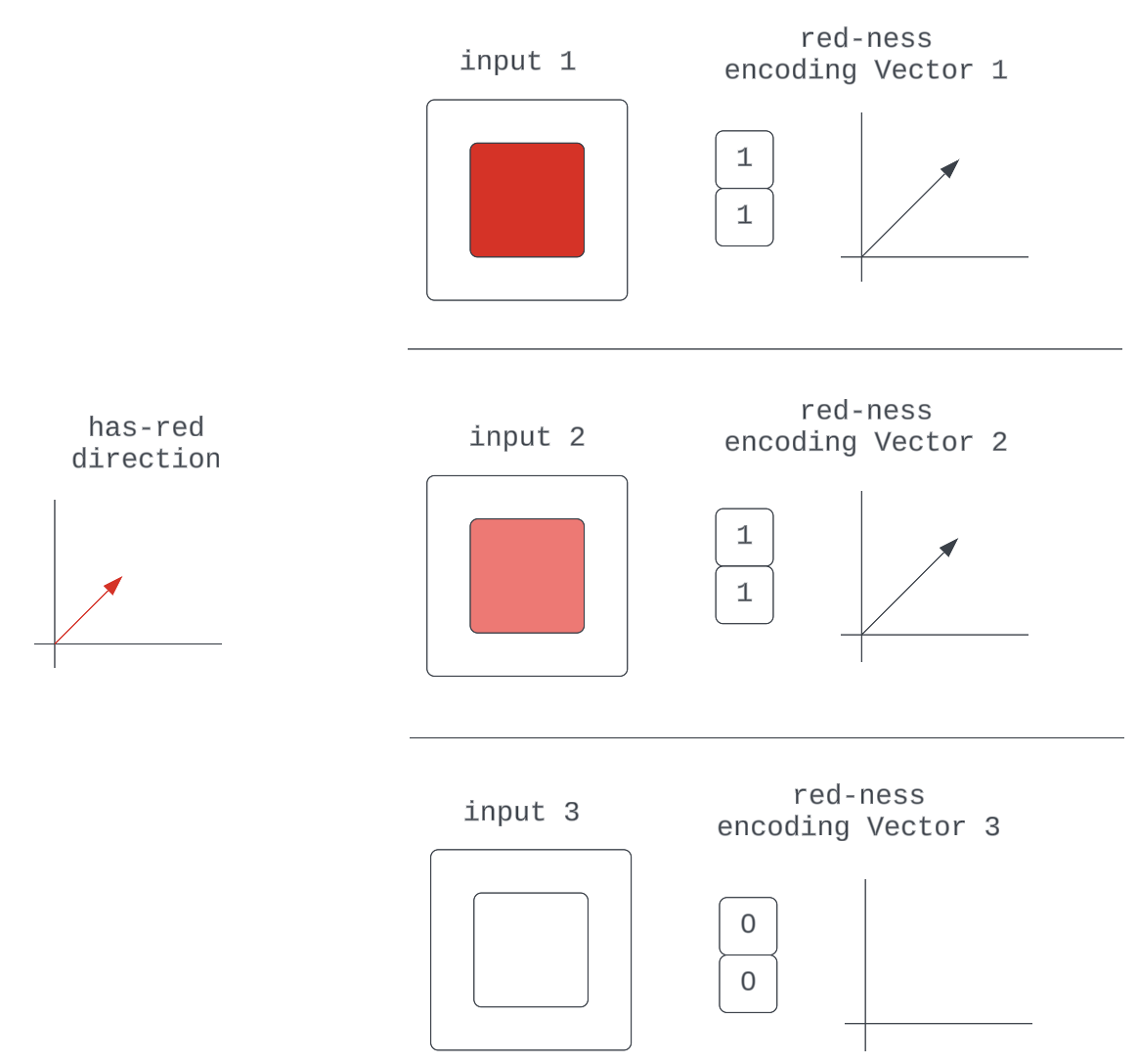
Determine 5: Numerous encoding vectors for the red-ness high quality within the enter
They’re all simply scaled representations of some elementary red-ness unit vector, which specifies route.
That is merely a generalization of the composability argument that claims neural networks can study to make their encodings of enter qualities “depth”-sensitive by scaling some attribute unit vector.
Different Impractical Encoding Regimes
Determine 6a
An alternate encoding scheme may very well be that each one we are able to get from fashions are binary encodings of properties; e.g., “The Pink values on this RGB enter are Non-zero.” That is clearly not very strong.
Determine 6b
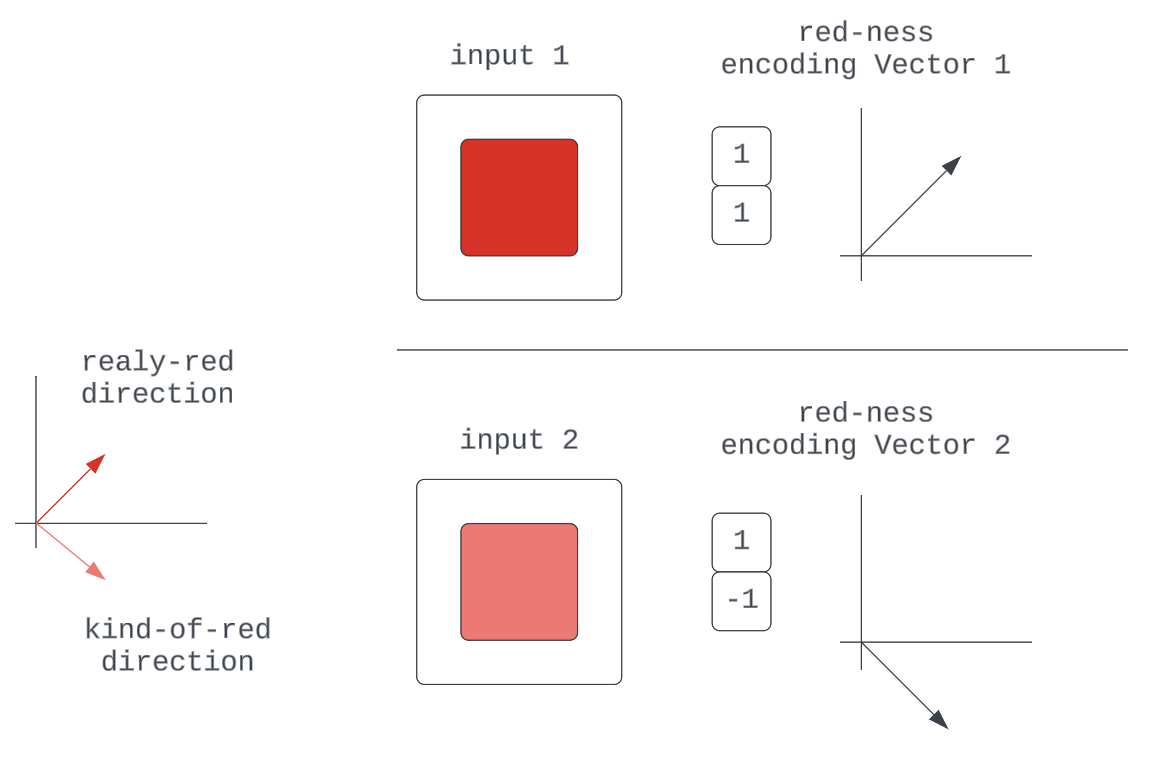
One other is that we have now a number of distinctive instructions for qualities that may very well be described by mere variations in scale of some extra elementary high quality: “One Neuron for “kind-of-red” for 0-127 within the RGB enter, one other for “really-red” for 128-255 within the RGB enter.” We’d run out of instructions pretty rapidly.
Declare #2: These Encodings Are Composed as a Vector Sum
Now, that is the stronger of the 2 claims as it isn’t essentially a consequence of something launched to date.
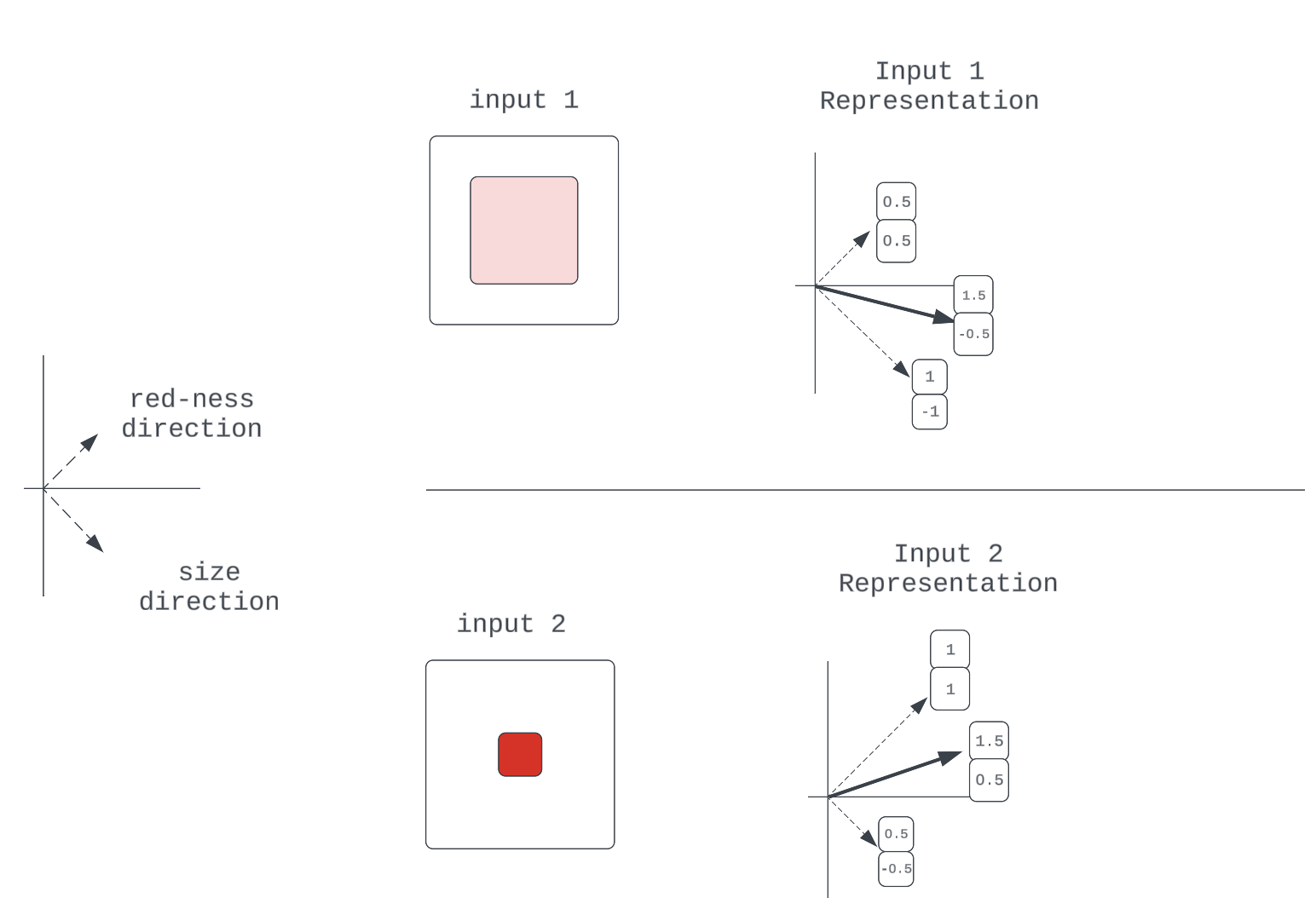
Determine 7: An instance of 2-property illustration
Notice: We assume independence between properties, ignoring the degenerate case the place a measurement of zero implies the colour isn’t crimson (nothing).
A vector sum may seem to be the pure (if not solely) factor a community might do to mix these encoding vectors. To understand why this declare is value verifying, it’ll be value investigating if different non-linear features might additionally get the job completed. Recall that the factor we would like is a perform that mixes these encodings at some part within the mannequin in a means that preserves data for downstream computation. So that is successfully an data compression drawback.
As mentioned in Elhage et al [3a], the next non-linear compression scheme might get the job completed:
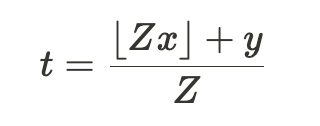
The place we search to compress values x and y into t. The worth of Z is chosen in accordance with the required floating-point precision wanted for compressions.
# A Python Implementation
from math import ground
def compress_values(x1, x2, precision=1):
z = 10 ** precision
compressed_val = (ground(z * x1) + x2) / z
return spherical(compressed_val, precision * 2)
def recover_values(compressed_val, precision=1):
z = 10 ** precision
x2_recovered = (compressed_val * z) - ground(compressed_val * z)
x1_recovered = compressed_val - (x2_recovered / z)
return spherical(x1_recovered, precision), spherical(x2_recovered, precision)
# Now to compress vectors a and b
a = [0.3, 0.6]
b = [0.2, 0.8]
compressed_a_b = [compress_values(a[0], b[0]), compress_values(a[1], b[1])]
# Returned [0.32, 0.68]
recovered_a, recovered_b = (
[x, y] for x, y in zip(
recover_values(compressed_a_b[0]),
recover_values(compressed_a_b[1])
)
)
# Returned ([0.3, 0.6], [0.2, 0.8])
assert all([recovered_a == a, recovered_b == b])As demonstrated, we’re capable of compress and get well vectors a and b simply nice, so that is additionally a viable means of compressing data for later computation utilizing non-linearities just like the ground() perform that neural networks can approximate. Whereas this appears somewhat extra tedious than simply including vectors, it exhibits the community does have choices. This requires some proof and additional arguments in assist of linearity.
Proof of Linearity
The usually-cited instance of a mannequin part exhibiting sturdy linearity is the embedding layer in language fashions [4], the place relationships like the next exist between representations of phrases:
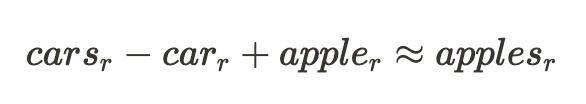
This instance would trace on the following relationship between the standard of $plurality$ within the enter phrases and the remainder of their illustration:
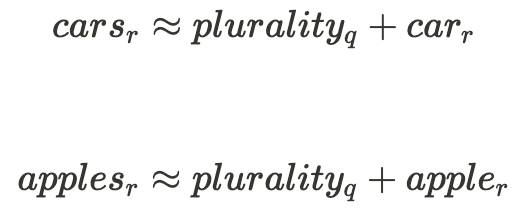
Okay, in order that’s some proof for one part in a kind of neural community having linear representations. The broad define of arguments for this being prevalent throughout networks is that linear representations are each the extra pure and performant [3b][3a] possibility for neural networks to decide on.
How Necessary for Interpretability Is It That This Is True?
If non-linear compression is prevalent throughout networks, there are two different regimes wherein networks might function:
- Computation remains to be largely completed on linear variables: On this regime, whereas the knowledge is encoded and moved between elements non-linearly, the mannequin elements would nonetheless decompress the representations to run linear computations. From an interpretability standpoint, whereas this wants some further work to reverse engineer the decompression operation, this would not pose too excessive a barrier.
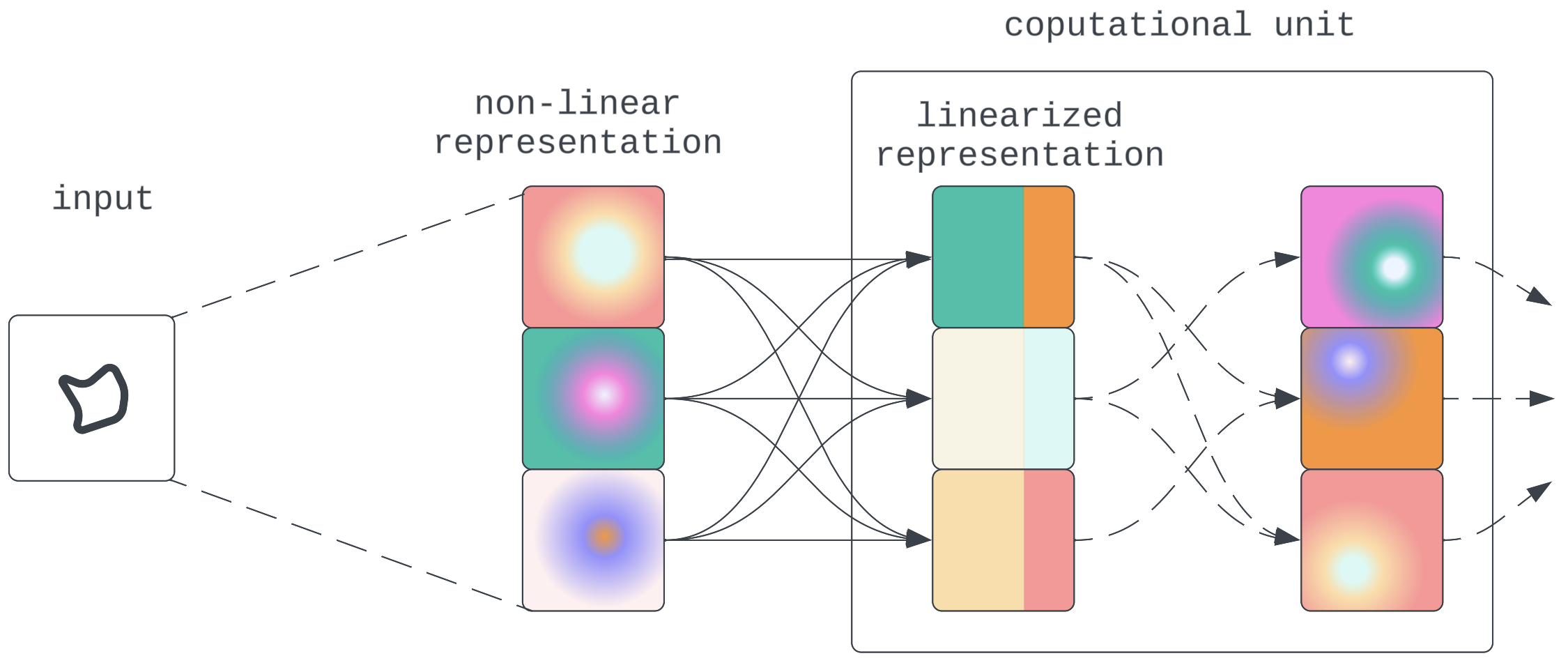Determine 8:Non-linear compression and propagation intervened by linear computation - Computation is completed in a non-linear state: The mannequin figures out a technique to do computations straight on the non-linear illustration. This might pose a problem needing new interpretability strategies. Nevertheless, based mostly on arguments mentioned earlier about mannequin structure affordances that is anticipated to be unlikely.
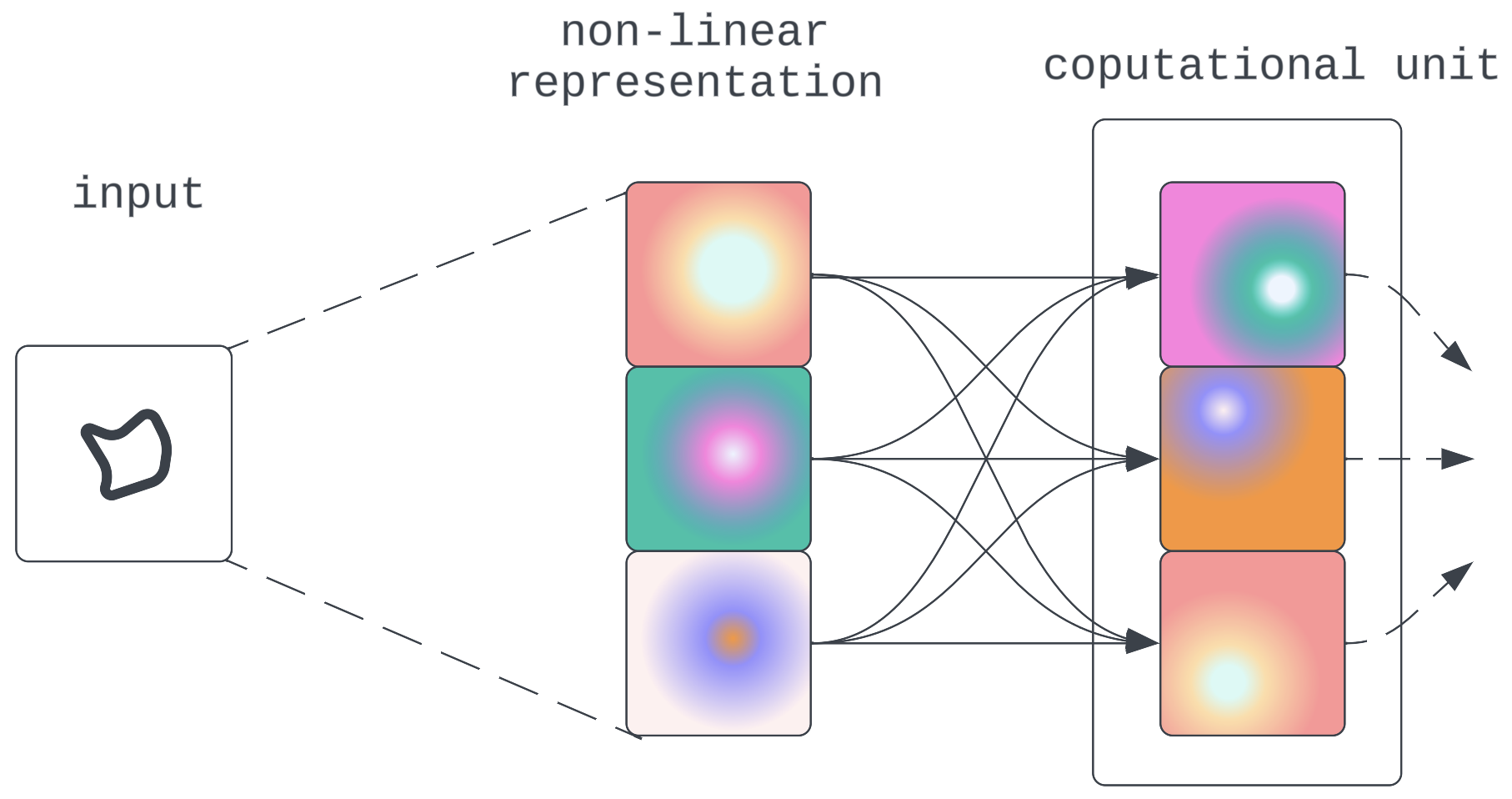
Determine 9: Direct non-linear computation
Options
As promised within the introduction, after avoiding the phrase “function” this far into the submit, we’ll introduce it correctly. As a fast apart, I feel the engagement of the analysis group on the subject of defining what we imply once we use the phrase “function” is without doubt one of the issues that makes mech interp, as a pre-paradigmatic science, thrilling. Whereas completely different definitions have been proposed [3c] and the ultimate verdict is in no way out, on this submit and others to come back on mech interp, I’ll be utilizing the next:
“The options of a given neural community represent a set of all of the enter qualities the community would dedicate a neuron to if it might.”
We’ve already mentioned the concept of networks essentially encoding discrete qualities of inputs, so essentially the most attention-grabbing a part of the definition is, “…would dedicate a neuron to if it might.”
What Is Meant by “…Dedicate a Neuron To…”?
In a case the place all quality-encoding instructions are distinctive one-hot vectors in activation house ([0, 1] and [1, 0], for instance) the neurons are stated to be basis-aligned; i.e., one neuron’s activation within the community independently represents the depth of 1 enter high quality.
Determine 10: Instance of a illustration with basis-aligned neurons
Notice that whereas adequate, this property isn’t vital for lossless compression of encodings with vector addition. The core requirement is that these function instructions be orthogonal. The rationale for this is identical as once we explored the non-linear compression technique: we need to fully get well every encoded function downstream.
Foundation Vectors
Following the Linearity speculation, we count on the activation vector to be a sum of all of the scaled function instructions:
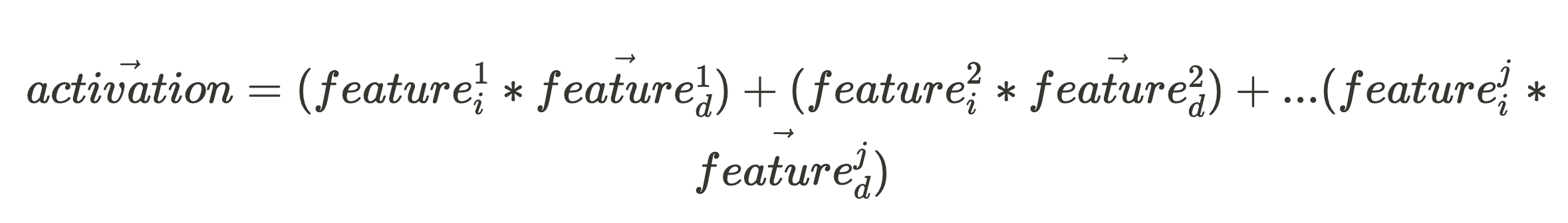
Given an activation vector (which is what we are able to straight observe when our community fires), if we need to know the activation depth of some function within the enter, all we’d like is the function’s unit vector, function^j_d: (the place the character “.” within the following expression is the vector dot product.)
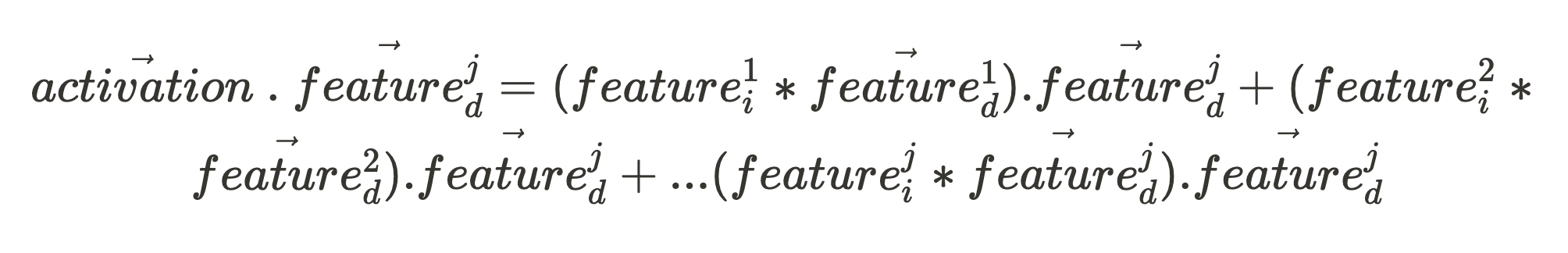
If all of the function unit vectors of that community part (making up the set, Features_d) are orthogonal to one another:
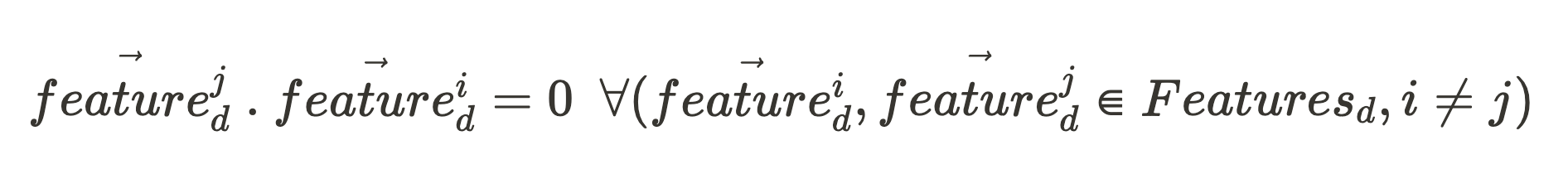
And, for any vector:
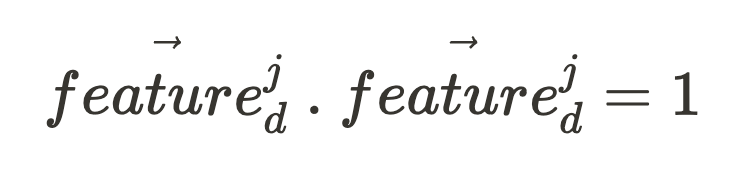
These simplify our equation to offer an expression for our function depth function^j_i:
Permitting us to totally get well our compressed function:
All that was to determine the perfect property of orthogonality between function instructions. This implies regardless that the concept of “one neuron firing by x-much == one function is current by x-much” is fairly handy to consider, there are different equally performant function instructions that don’t have their neuron-firing patterns aligning this cleanly with function patterns. (As an apart, it seems basis-aligned neurons don’t occur that usually. [3d])
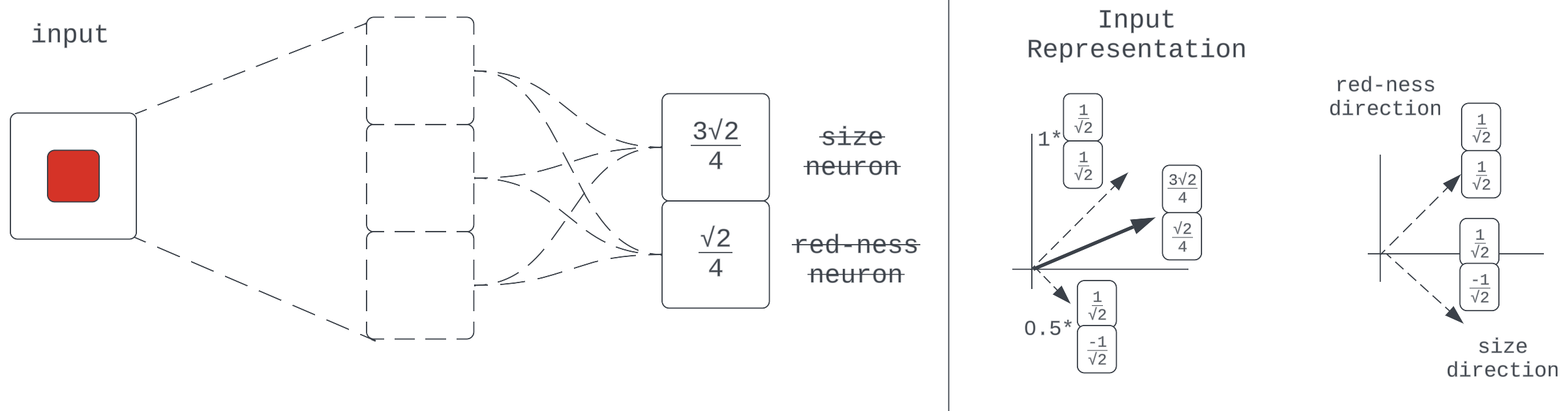
Fig 11: Orthogonal function instructions from non-basis-aligned neurons
With this context, the request: ”dedicate a neuron to…” may appear arbitrarily particular. Maybe “dedicate an additional orthogonal route vector” can be adequate to accommodate a further high quality. However as you most likely already know, orthogonal vectors in an area don’t develop on timber. A 2-dimensional house can solely have 2 orthogonal vectors at a time, for instance. So to make extra room, we would want an additional dimension, i.e [X X] -> [X X X] which is tantamount to having an additional neuron devoted to this function.
How Are These Options Saved in Neural Networks?
To the touch grass rapidly, what does it imply when a mannequin part has realized 3 orthogonal function instructions {[1 0 0], [0 1 0], [0 0 1]} for compressing an enter vector [a b c]?
To get the compressed activation vector, we count on a collection of dot merchandise with every function route to get our function scale.
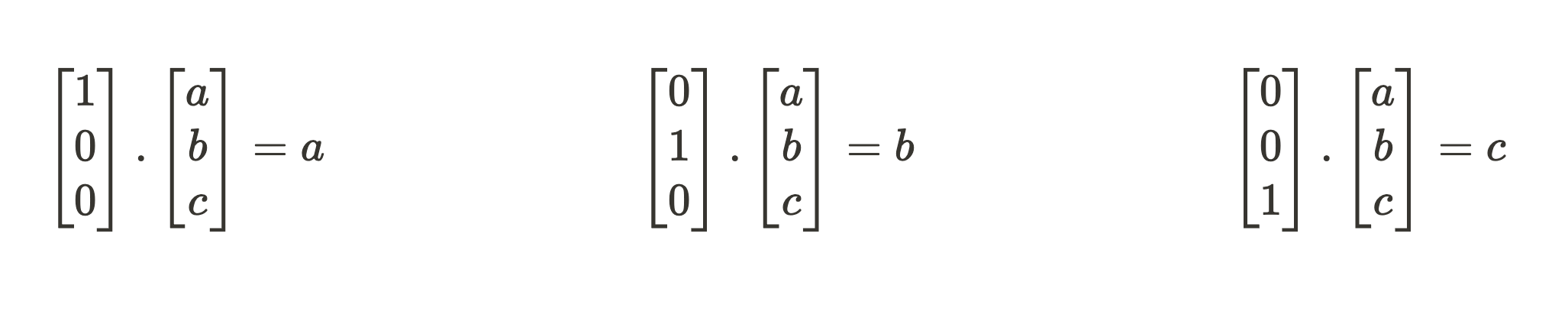
Now we simply should sum up our scaled-up function instructions to get our “compressed” activation state. On this toy instance, the options are simply the vector values so lossless decompressing will get us what we began with.
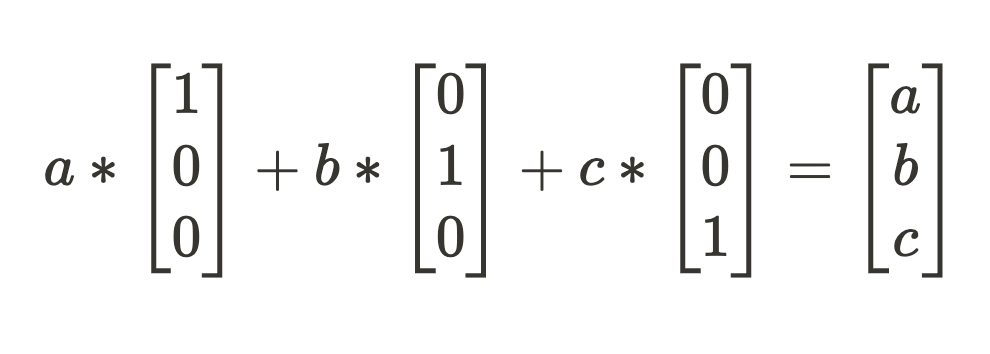
The query is: what does this appear to be in a mannequin? The above sequence of transformations of dot merchandise adopted by a sum is equal to the operations of the deep studying workhorse: matrix multiplication.
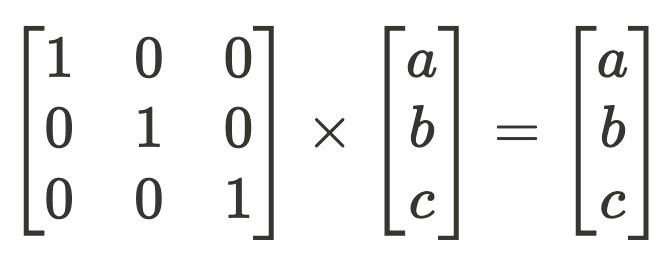
The sooner sentence, “…a mannequin part has realized 3 orthogonal function instructions,” ought to have been a giveaway. Fashions retailer their learnings in weights, and so our function vectors are simply the rows of this layer’s realized weight matrix, W.
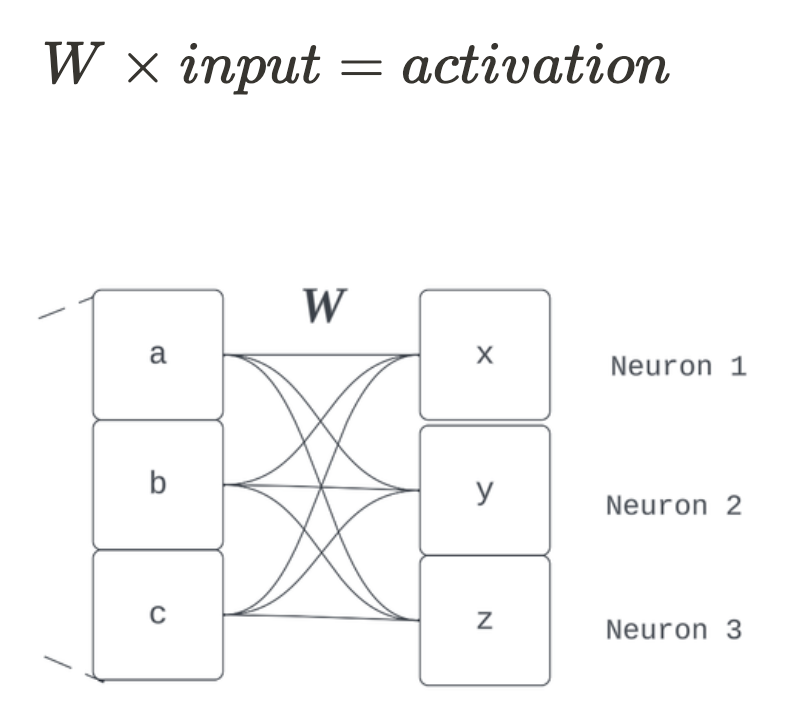
Why didn’t I simply say the entire time, “Matrix multiplication. Finish of part.” As a result of we don’t at all times have toy issues in the true world. The realized options aren’t at all times saved in only one set of weights. It might (and often does) contain an arbitrarily lengthy sequence of linear and non-linear compositions to reach at some function route (however the important thing perception of decompositional linearity is that this computation might be summarised by a route used to compose some activation). The promise of linearity we mentioned solely has to do with how function representations are composed. For instance, some arbitrary vector is extra prone to not be hanging round for discovery by simply studying one row of a layer’s weight matrix, however the computation to encode that function is unfold throughout a number of weights and mannequin elements. So we needed to handle options as arbitrary unusual instructions in activation house as a result of they usually are. This level brings the proposed dichotomy between illustration and algorithmic interpretability into query.
Again to our working definition of options:
“The options of a given neural community represent a set of all of the enter qualities the community would dedicate a neuron to if it might.”
On the Conditional Clause: “…Would Dedicate a Neuron to if It Might…”
You possibly can consider this definition of a function as a little bit of a set-up for an introduction to a speculation that addresses its counterfactual: What occurs when a neural community can not present all its enter qualities with devoted neurons?
Superposition
Up to now, our mannequin has completed nice on the duty that required it to compress and propagate 2 realized options — “measurement” and “red-ness” — by a 2-dimensional layer. What occurs when a brand new job requires the compression and propagation of a further function just like the x-displacement of the middle of the sq.?
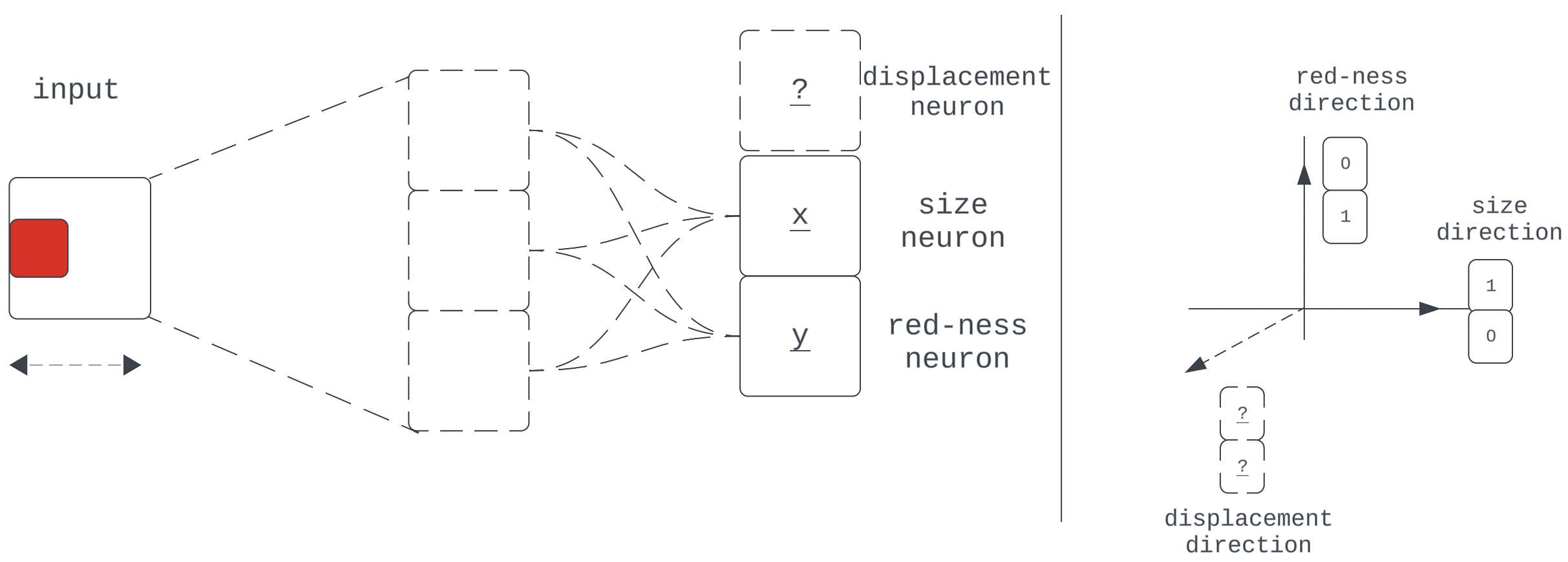
Determine 12
This exhibits our community with a brand new job, requiring it to propagate yet another realized property of the enter: middle x-displacement. We’ve returned to utilizing neuron-aligned bases for comfort.
Earlier than we go additional with this toy mannequin, it will be value pondering by if there are analogs of this in massive real-world fashions. Let’s take the big language mannequin GPT2 small [5]. Do you assume, if you happen to had all week, you possibly can consider as much as 769 helpful options of an arbitrary 700-word question that might assist predict the subsequent token (e.g., “is a proper letter,” “comprises what number of verbs,” “is about about ‘Chinua Achebe,’” and so forth.)? Even when we ignored the truth that function discovery was one of many identified superpowers of neural networks [c] and assumed GPT2-small would additionally find yourself with solely 769 helpful enter options to encode, we’d have a scenario very similar to our toy drawback above. It’s because GPT2 has —on the narrowest level in its structure— solely 768 neurons to work with, identical to our toy drawback has 2 neurons however must encode details about 3 options. [d]
So this complete “mannequin part encodes extra options it has neurons” enterprise ought to be value trying into. It most likely additionally wants a shorter identify. That identify is the Superposition speculation. Contemplating the above thought experiment with GPT2 Small, it will appear this speculation is simply stating the obvious- that fashions are one way or the other capable of symbolize extra enter qualities (options) than they’ve dimensions for.
What Precisely Is Hypothetical About Superposition?
There’s a purpose I launched it this late within the submit: it will depend on different abstractions that are not essentially self-evident. An important is the prior formulation of options. It assumes linear decomposition- the expression of neural web representations as sums of scaled instructions representing discrete qualities of their inputs. These definitions may appear round, however they’re not if outlined sequentially:
In the event you conceive of neural networks as encoding discrete data of inputs referred to as Options as instructions in activation house, then once we suspect the mannequin has extra of those options than it has neurons, we name this Superposition.
A Approach Ahead
As we’ve seen, it will be handy if the options of a mannequin had been aligned with neurons and vital for them to be orthogonal vectors to permit lossless restoration from compressed representations. So to counsel this is not taking place poses difficulties to interpretation and raises questions on how networks can pull this off anyway.
Additional improvement of the speculation supplies a mannequin for occupied with why and the way superposition occurs, clearly exposes the phenomenon in toy issues, and develops promising strategies for working round obstacles to interpretability [6]. Extra on this in a future submit.
Footnotes
[a] That’s, algorithms extra descriptive than “Take this Neural Web structure and fill in its weights with these values, then do a ahead move.”
[b] Primarily from concepts launched in Toy Models of Superposition
[c] This refers particularly to the codification of options as their superpower. People are fairly good at predicting the subsequent token in human textual content; we’re simply not good at writing packages for extracting and representing this data vector house. All of that’s hidden away within the mechanics of our cognition.
[d] Technically, the quantity to check the 768-dimension residual stream width to is the utmost variety of options we predict *any* single layer must cope with at a time. If we assume equal computational workload between layers and assume every batch of options was constructed based mostly on computations on the earlier, for the 12-layer GPT2 mannequin, this might be 12 * 768 = 9,216 options you’d must assume up.
References
[1] Chris Olah on Mech Interp – 80000 Hours
[3] Toy Models of Superposition
[3c] What are Features?
[3d] Definitions and Motivation
[4] Linguistic regularities in continuous space word representations: Mikolov, T., Yih, W. and Zweig, G., 2013. Proceedings of the 2013 convention of the North American chapter of the Affiliation for Computational Linguistics: Human language applied sciences, pp. 746–751.
[5] Language Models are Unsupervised Multitask Learners: Alec Radford, Jeffrey Wu, Rewon Little one, David Luan, Dario Amodei, Ilya Sutskever
[6] Towards Monosemanticity: Decomposing Language Models With Dictionary Learning
